mglsadf
Functions
-
int main(int argc, char *argv[])
mglsadf [ option ] mgcfile [ infile ]
-m int
order of coefficients \((0 \le M)\)
-a double
all-pass constant \((|\alpha| < 1)\)
-c int
gamma \(\gamma = -1 / C\) \((1 \le C)\)
-p int
frame period \((1 \le P)\)
-i int
interpolation period \((0 \le I \le P/2)\)
-P int
order of Pade approximation \((4 \le L \le 7)\)
-t
transpose filter
-k
filtering without gain
mgcfile str
double-type mel-generalized cepstral coefficients
infile str
double-type input sequence
stdout
double-type output sequence
In the below example, an excitation signal generated from pitch information is passed through the MLSA filter built from mel-cepstral coefficients
data.mcep.excite < data.pitch | mglsadf data.mcep > data.syn
- Parameters:
argc – [in] Number of arguments.
argv – [in] Argument vector.
- Returns:
0 on success, 1 on failure.
-
class MlsaDigitalFilter
Apply MLSA digital filter for speech synthesis to signals.
The transfer function \(H(z)\) of an MLSA filter is
\[\begin{split}\begin{eqnarray} H(z) &=& \exp \sum_{m=0}^M b(m) \varPhi_m(z) \\ &\equiv& K \cdot D(z) \end{eqnarray}\end{split}\]where\[\begin{split} \varPhi_m(z) = \left\{ \begin{array}{ll} 1, & m = 0 \\ \dfrac{(1-\alpha^2)z^{-1}}{1-\alpha z^{-1}} \tilde{z}^{-(m-1)}, & m \ge 1 \end{array} \right. \end{split}\]and\[\begin{split}\begin{eqnarray} K &=& \exp \, b(0), \\ D(z) &=& \exp \sum_{m=1}^M b(m) \varPhi_m(z). \end{eqnarray}\end{split}\]The filter \(D(z)\) can be implemented by approximating exponential function as an \(L\)-th order rational function \(R_L(\cdot)\) using the modified Pade approximation:\[ D(z) = \exp F(z) \simeq R_L(F(z)). \]The block diagram of the basic filter \(F(z)\) is shown as below.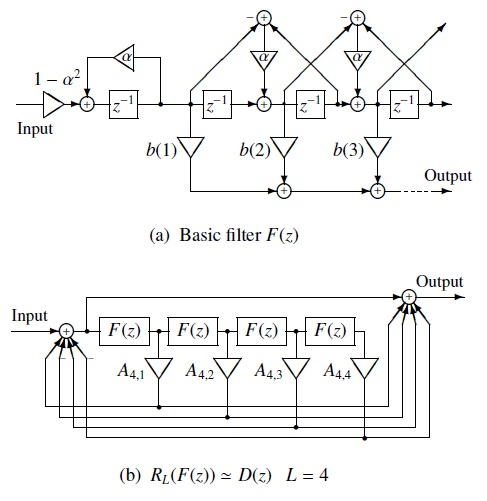
To improve the accuracy of the approximation, the basic filter is decomposed as
\[ F(z) = F_1(z) + F_2(z) \]where\[\begin{split}\begin{eqnarray} F_1(z) &=& b(1) \varPhi_1(z), \\ F_2(z) &=& \exp \sum_{m=2}^M b(m) \varPhi_m(z). \end{eqnarray}\end{split}\]Given the \(M\)-th order MLSA filter coefficients,
\[ \begin{array}{cccc} b(0), & b(1), & \ldots, & b(M), \end{array} \]an output signal is obtained by applying \(H(z)\) to an input signal in time domain.Public Functions
-
MlsaDigitalFilter(int num_filter_order, int num_pade_order, double alpha, bool transposition)
- Parameters:
num_filter_order – [in] Order of filter coefficients, \(M\).
num_pade_order – [in] Order of Pade approximation, \(L\).
alpha – [in] All-pass constant, \(\alpha\).
transposition – [in] If true, use transposed form filter.
-
inline int GetNumFilterOrder() const
- Returns:
Order of coefficients.
-
inline int GetNumPadeOrder() const
- Returns:
Order of Pade approximation.
-
inline double GetAlpha() const
- Returns:
All-pass constant.
-
inline bool GetTranspositionFlag() const
- Returns:
True if transposed form is used.
-
inline bool IsValid() const
- Returns:
True if this object is valid.
-
bool Run(const std::vector<double> &filter_coefficients, double filter_input, double *filter_output, MlsaDigitalFilter::Buffer *buffer) const
- Parameters:
filter_coefficients – [in] \(M\)-th order MLSA filter coefficients.
filter_input – [in] Input signal.
filter_output – [out] Output signal.
buffer – [inout] Buffer.
- Returns:
True on success, false on failure.
-
bool Run(const std::vector<double> &filter_coefficients, double *input_and_output, MlsaDigitalFilter::Buffer *buffer) const
- Parameters:
filter_coefficients – [in] \(M\)-th order MLSA filter coefficients.
input_and_output – [inout] Input/output signal.
buffer – [inout] Buffer.
- Returns:
True on success, false on failure.
-
class Buffer
Buffer for MlsaDigitalFilter class.
-
MlsaDigitalFilter(int num_filter_order, int num_pade_order, double alpha, bool transposition)
-
class MglsaDigitalFilter
Apply MGLSA digital filter for speech synthesis to signals.
The transfer function \(H(z)\) of an MLSA filter is
\[\begin{split}\begin{eqnarray} H(z) &=& s_\gamma^{-1} \left( \sum_{m=0}^M b'_\gamma(m) \varPhi_m(z) \right) \\ &\equiv& K \cdot D(z) \end{eqnarray}\end{split}\]where\[\begin{split} \varPhi_m(z) = \left\{ \begin{array}{ll} 1, & m = 0 \\ \dfrac{(1-\alpha^2)z^{-1}}{1-\alpha z^{-1}} \tilde{z}^{-(m-1)}, & m \ge 1 \end{array} \right. \end{split}\]and\[\begin{split}\begin{eqnarray} K &=& s_\gamma^{-1} \left( b'_\gamma(0) \right), \\ D(z) &=& s_\gamma^{-1} \left(\sum_{m=1}^M b'_\gamma(m) \varPhi_m(z)\right). \end{eqnarray}\end{split}\]The filter \(D(z)\) is implemented by cascading filter \(1/B(z)\):\[\begin{split}\begin{eqnarray} D(z) &=& \left( \frac{1}{B(z)} \right)^C \\ &=& \left( \frac{1} {1 + \gamma \sum_{m=1}^M b'_\gamma(m) \varPhi_m(z)} \right)^C . \end{eqnarray}\end{split}\]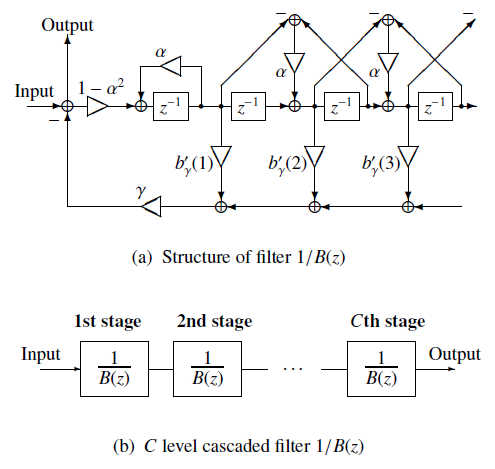
The filter coeffcients \(b'_\gamma(m)\) are obtained by applying gain normalization to the MLSA filter coefficients:
\[ \begin{array}{cccc} b(0), & b(1), & \ldots, & b(M). \end{array} \]An output signal is obtained by applying \(H(z)\) to an input signal in time domain.Public Functions
-
MglsaDigitalFilter(int num_filter_order, int num_pade_order, int num_stage, double alpha, bool transposition)
- Parameters:
num_filter_order – [in] Order of filter coefficients, \(M\).
num_pade_order – [in] Order of Pade approximation, \(L\).
num_stage – [in] Number of stages, \(C\). If zero, MLSA filter is used.
alpha – [in] All-pass constant, \(\alpha\).
transposition – [in] If true, use transposed form filter.
-
inline int GetNumFilterOrder() const
- Returns:
Order of coefficients.
-
inline int GetNumPadeOrder() const
- Returns:
Order of Pade approximation.
-
inline int GetNumStage() const
- Returns:
Number of stages.
-
inline double GetAlpha() const
- Returns:
All-pass constant.
-
inline bool GetTranspositionFlag() const
- Returns:
True if transposed form is used.
-
inline bool IsValid() const
- Returns:
True if this object is valid.
-
bool Run(const std::vector<double> &filter_coefficients, double filter_input, double *filter_output, MglsaDigitalFilter::Buffer *buffer) const
- Parameters:
filter_coefficients – [in] \(M\)-th order MGLSA filter coefficients.
filter_input – [in] Input signal.
filter_output – [out] Output signal.
buffer – [inout] Buffer.
- Returns:
True on success, false on failure.
-
bool Run(const std::vector<double> &filter_coefficients, double *input_and_output, MglsaDigitalFilter::Buffer *buffer) const
- Parameters:
filter_coefficients – [in] \(M\)-th order MGLSA filter coefficients.
input_and_output – [inout] Input/output signal.
buffer – [inout] Buffer.
- Returns:
True on success, false on failure.
-
class Buffer
Buffer for MglsaDigitalFilter class.
-
MglsaDigitalFilter(int num_filter_order, int num_pade_order, int num_stage, double alpha, bool transposition)