dtw

Functions

int main(int argc, char *argv[])

dtw [ option ] file1 [ infile ]

• -l int

  • length of vector \((1 \le M+1)\)

• -m int

  • order of vector \((0 \le M)\)

• -p int

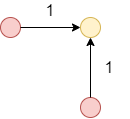
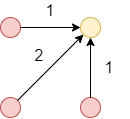
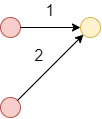
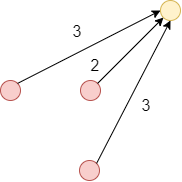
  • type of local path constraints \((0 \le P \le 6)\)

• -d int

  • distance metric

    • 0 Manhattan

    • 1 Euclidean

    • 2 squared Euclidean

    • 3 symmetric Kullback-Leibler

• -P str

  • int-type Viterbi path

• -S str

  • double-type DTW score

• file1 str

  • double-type reference vector sequence

• infile str

  • double-type query vector sequence

• stdout

  • double-type concatenated vector sequence

Parameters:

• argc – [in] Number of arguments.

• argv – [in] Argument vector.

Returns:

0 on success, 1 on failure.

See also

dtw_merge

class DynamicTimeWarping

Perform dynamic time warping.

The input is the \(M\)-th order query vectors:

\[ \begin{array}{cccc} \boldsymbol{x}(1), & \boldsymbol{x}(2), & \ldots, & \boldsymbol{x}(T_x), \end{array} \]

and the \(M\)-th order reference vectors:

\[ \begin{array}{cccc} \boldsymbol{y}(1), & \boldsymbol{y}(2), & \ldots, & \boldsymbol{y}(T_y), \end{array} \]

where \(T_x\) and \(T_y\) are the length of the each vectors. The output is the concatenated vector sequence:

\[ \begin{array}{cccc} \boldsymbol{z}(1), & \boldsymbol{z}(2), & \ldots, & \boldsymbol{z}(T), \end{array} \]

where

\[\begin{split} \boldsymbol{z}(t) = \left[ \begin{array}{c} \boldsymbol{x}(\phi_x(t)) \\ \boldsymbol{y}(\phi_y(t)) \end{array} \right], \end{split}\]

and \(\phi_x(\cdot)\) and \(\phi_y(\cdot)\) are the function which maps the Viterbi time index into the corresponding time index of query/reference data sequence, respectively.

Public Types

enum LocalPathConstraints

Local path constraints.

Values:

enumerator kType0

enumerator kType1

enumerator kType2

Require \(T_x >= T_y\).

enumerator kType3

enumerator kType4

enumerator kType5

enumerator kType6

enumerator kNumTypes

Public Functions

DynamicTimeWarping(int num_order, LocalPathConstraints local_path_constraint, DistanceCalculation::DistanceMetrics distance_metric)

Parameters:

• num_order – [in] Order of vector, \(M\).

• local_path_constraint – [in] Type of local path constraint.

• distance_metric – [in] Distance metric.

inline int GetNumOrder() const

Returns:

Order of vector.

inline LocalPathConstraints GetLocalPathConstraint() const

Returns:

Type of local path constraint.

inline DistanceCalculation::DistanceMetrics GetDistanceMetric() const

Returns:

Distance metric.

inline bool IsValid() const

Returns:

True if this object is valid.

bool Run(const std::vector<std::vector<double>> &query_vector_sequence, const std::vector<std::vector<double>> &reference_vector_sequence, std::vector<std::pair<int, int>> *viterbi_path, double *total_score) const

Parameters:

• query_vector_sequence – [in] \(M\)-th order query vectors. The shape is \([T_x, M+1]\).

• reference_vector_sequence – [in] \(M\)-th order reference vectors. The shape is \([T_y, M+1]\).

• viterbi_path – [out] Best sequence of the pairs of index.

• total_score – [out] Score of dynamic time warping.

Returns:

True on success, false on failure.

class DistanceCalculation

Calculate distance between two vectors.

Public Types

enum DistanceMetrics

Metric of distance

Values:

enumerator kManhattan

enumerator kEuclidean

enumerator kSquaredEuclidean

enumerator kSymmetricKullbackLeibler

enumerator kNumMetrics

Public Functions

DistanceCalculation(int num_order, DistanceMetrics distance_metric)

Parameters:

• num_order – [in] Order of vector, \(M\).

• distance_metric – [in] Distance metric.

inline int GetNumOrder() const

Returns:

Order of vector.

inline DistanceMetrics GetDistanceMetric() const

Returns:

Distance metric.

inline bool IsValid() const

Returns:

True if this object is valid.

bool Run(const std::vector<double> &vector1, const std::vector<double> &vector2, double *distance) const

Parameters:

• vector1 – [in] \(M\)-th order vector.

• vector2 – [in] \(M\)-th order vector.

• distance – [out] Distance between the two vectors.

Returns:

True on success, false on failure.